最近在知乎上看到一个挺有意思的提问:赌场是有没有办法必赢呢?提出如下的策略
可能这也是很多人长久以来心中的疑惑,上述策略看似很合理,可转念一想赌场那么精明,怎么会让赌徒这么容易赢钱呢。这里我用模拟仿真的方法,完全基于理性客观数据,分析下赌博到底能不能赚钱?
1、情景回顾
每次下注的金额都是之前输的金额的 2.5 倍,赢钱后再从 1 元开始投,往复循环。
也就是说,输钱就一直继续投入,赢钱就结束;再重新开启另外一个循环。
不过这里也有一些未确定的 2 个信息:赢钱概率多少,本金上限多少?因为这很可能严重影响最终的结果,所以我会在后续模型中对这两个变量进行分析
2、模拟方法
使用 Python 语言,使用 random 库产生随机数进行模拟(每一次赌博都可以视为一次随机,我们这里暂不考虑赌场可能存在的黑箱操作)
以下列举了连续投注需要的本金值(为显示效果,取整),可看到虽然初始只要 1 元,但随着投注次数的增多,本金高的恐怖!

3、赌场基本情况一览
我们先简单看一下 50%概率赢钱、本金 1 万元的收益,正态分布结果如下(测试 1 万次)。
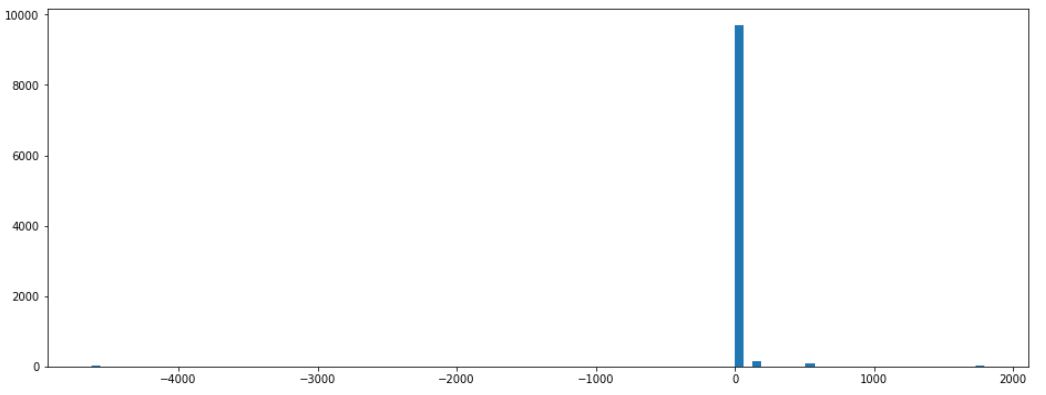
横轴是赢的钱数,纵轴是次数
从图中可以看到,这 1 万次测试中 9000+次数是赢钱的(1 元),个别情况会赢或输更多的钱。为验证这个结果准确性,又测试了 10 万次,还是同样的结论。
那是不是可以得到结论,赌博大概率是可以赢钱的?对,的确是大概率可以赢钱。但是,得注意一个问题,虽然赢钱概率大,但是只能赢 1 元啊,若输了可是好几千呢。那现在就有疑问了,赢钱概率大但是每次赢得少,输钱概率低但是每次输得多,那综合来看(即数学期望)是赢还是输呢?
那么,接下来我们看看在不同本金、赢钱概率下,来测试到底是输还是赢。
4、不同本金下的赌博
由于本金的多少,会影响可投注的次数,我们来模拟下本金 100 元-100 万元(每 100 元递进)赌博的情景。每种情况重复则是 1 万次,取赌徒赢钱概率为 50%
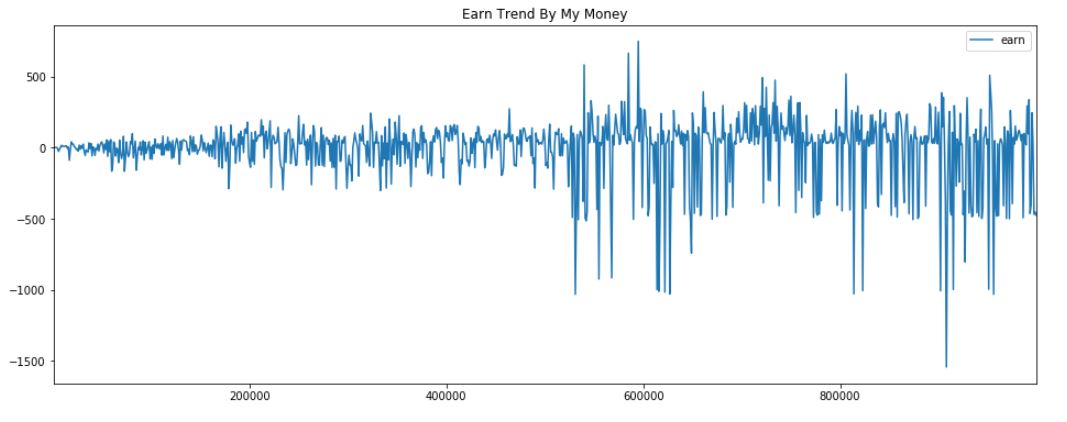
横轴是投入的本金,纵轴是一万次收益的平均值
- 本金从 100 到 100 万,其收益一直在 0 附件波动(从具体数据上看,在 1 附近波动)
- 随着本金的加大,波动越来越大;
- 向下的波动,比向上的波动强烈
因此我们可以得到的结论是,无论本金是多少钱,大概率收益仍在初始值,且赚大钱要比输大钱更难。
5、不同胜率的赌博
以上所有的分析,都是基于赌场和客人在同等胜率的情况。在现实情况下,很多人甚至会怀疑赌场是否有一些黑科技,会让赌场更容易赚钱,而赌徒更容易赔钱。那接下来,我们再看一下赌徒不同赢钱概率下的收益情况。这里假设本金是 1 万元,赌徒赢钱概率 10%-90%,同样重复模拟 1 万次得到均值图如下。
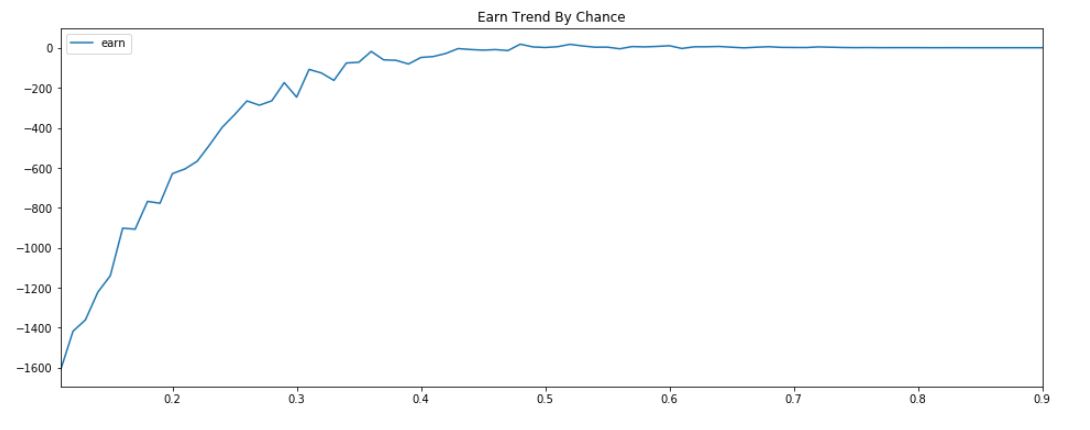
横轴是赌徒赢钱概率,纵轴是一万次收益的平均值
- 当胜率在 50%以下时,随着赌徒胜率的提升,收益急剧增加,但均为负值,即赌徒这时是赔钱的
- 当胜率在 50%以上时,赌徒收益逐渐趋于 0(具体数字是 1)
结论并不是如我们想象中那样,赌徒与赌场的风险收益并没有互相对称。真实情况是,赌徒胜率越低则赔得越多,但即使胜率调高了,赌徒也不会赚太多钱。赌徒的收益与风险不成比例,高风险低收益!
6、结论
- 即使在赌场完全公平公正公开的情况下,赌徒也难以赚到很多钱。虽然说赌徒有很大概率赚到一丁点钱,但是这与承担的风险是非常不匹配的。在这场风险与收益不成比例的博弈中,明显赌场是胜利者
- 若赌场在赌博中有些许作弊,那对于赌客来说更是严重的打击,大概率连那一丁点的钱都不会赚到,只会输得倾家荡产~
- 以上的分析完全建立在理性的基础上,而实际操作中再掺杂各种不理性、冲动,只会让结果更加往坏的方向发展。




